24 + 8 = 1500
Heinz und Michel im Gespräch über Rechendynamik
Heinz: Hallo Michel, gut das ich dich treffe…
Michel: Hi Heinz, wie gehts Dir?
H.: Gut. Sag mal, du bist doch technisch auf dem laufenden bezüglich Audioprozessoren und so.
M.: Hmm, geht so…
H.: Na, stell dein Licht mal nicht zu sehr unter den Scheffel. Also, ich hab´ da in einer Anzeige eines Hersteller von digitalen Kreuzschienen gelesen, sein Gerät hätte „1500 dB Rechendynamik“. Was heißt denn das?
M.: Nun, das bezieht sich auf die verwendeten DSPs und deren Rechenumfang.
H.: Kannst du das für einen normal Sterblichen erklären?
M.: Ich versuchs. Sicherlich weißt du was DSPs sind?
H.: Klar, digitale Signalprozessoren.
M.: Richtig. Wenn man sie näher betrachtet sind es eigentlich nur Rechenknechte, die Zahlen addieren, subtrahieren, multiplizieren usw.
H.: Und wenn es falsch ist: radieren.
M.: Äh, ja. Im digitalen wird ja mit Bits gerechnet, also im dualen Zahlensystem. Jeder dieser DSPs arbeitet bis zu einer bestimmten Zahlengröße, die durch seine Architektur der Hardware fest vorgegeben ist. Einer der zur Zeit typischen Vertreter hat z. B. eine Auflösung von 24 + 8 Bit.
H.: Ergibt 32…
M.: Falsch. Die beiden Zahlen stehen für die Mantisse und den Exponenten.
H.: Oh Gott, Mathe!
M.: Leider ja. Also, die erste Zahl gibt die Anzahl der Bits für die eigentliche Zahl, die zweite die Größe für die Zweier-Potenz an. Somit ist die größte Zahl, die so ein DSP behandeln könnte 2 hoch 24 mal 2 hoch 8. Das ergibt ca. 4,3 Billionen.
H.: Ist ja irre groß! Und wie kommt man jetzt auf diesen dB-Wert?
M.: Tja, da gibt es eine Formel die folgendermaßen aussieht (kramt ein Fachmagazin hervor und zeigt H. eine Formel): Wenn du hier nun unsere Zahlen 24 für wm und 8 für we einsetzt, kommst du auf 1529 dB.
![]()
H.: Wahnsinn! Das heißt ja, daß ich in einem digitalen Audioprozessor einen gigantischen Signal-Rauschabstand habe.
M.: Schön wär´s, aber dieser Wert ist leider nur theoretisch.
H.: Oh, und wieso?
M.: Nun, das erkläre ich Dir am besten an einem Beispiel. Wir werden dabei im Dezimalsystem bleiben, daß ist für uns Menschen einfacher zu rechnen. Addiere doch mal die beiden Zahlen 18 und 43 (M. kritzelt die Zahlen auf ein Stück Papier und reicht es H.).
H.: Das ist sogar für mich einfach, das ergibt 61.
M.: Und wie hast du das, wenn du es genau erklären müßtest, gemacht?
H.: Nun, zuerst addierte ich hinten die 8 und die 3, gibt 1 mit 1 im Sinn, und dann vorne die 1 plus die 4 plus die 1 vom Übertrag, ergibt 6.
M.: Prima, prinzipiell macht es ein DSP genauso. Nehmen wir aber mal an, wir hätten nur maximal zwei Stellen zur Verfügung und die Zahlen würden 87 und 46 lauten.
H.: Das Ergebnis wäre 133…ah ja, für die 1 vorne ist kein Platz mehr da, das kann man mit den zwei Stellen nicht mehr erfassen.
M.: Genau, deswegen besitzt ein DSP einen Exponenten, der den Zahlenbereich erweitert. Leider hat die Sache einen Pferdefuß.
H.: Und der wäre?
M.: Okay, nehmen wir zu unserer zweistelligen Mantisse noch einen dreistelligen Exponenten dazu. Addiere jetzt nochmal die Zahlen 87 und 46.
H.: Äh, das ergibt weiterhin 133.
M.: Ja, aber wir haben nur zwei Stellen. Also müssen wir das Ergebnis nun auf dieses Format bringen. Dazu verschieben wir eine Stelle in den Exponenten, was dann eine Multiplikation der Mantisse mit der Zahl 10 bedeutet. Wegen dieser Verschiebung wird dieses System auch Gleitkomma-Darstellung genannt. Das Ergebnis lautet dann 13 mit dem Exponenten 1, oder mathematisch gesagt: 13 E1.
H.: Ja, aber da fehlt doch eine 3!
M.: …und genau das ist der Pferdefuß! Unser Ergebnis hat also einen „Rundungsfehler“ von 0,3 E1, da wir ja keine Nachkommastellen haben, und das ergibt die Zahl 3.
H.: Also rechnet ein DSP falsch?
M.: Nicht gerade falsch, aber diese Rundungsfehler lassen sich nicht vermeiden und somit entstehen selbst in einem digitalem Audiogerät, zwar weniger als in einem analogen, Rauschen und Verzerrungen. Das Beispiel zeigt übrigens auch, das dieser Rundungsfehler trotz genügend Stellen im Exponenten entsteht.
H.: Also brauchen wir mehr Stellen in der Mantisse, oder?
M.: Perfekt analysiert! Um Rundungsfehler zu vermeiden und somit den Signal-Rauschabstand zu verbessern ist die Größe der Mantisse entscheidend und nicht die des Exponenten. Ergo wird unsere 24 + 8 DSP niemals einen besseren Wert als 144 dB erreichen…
H.: …denn das ist der Signal-Rauschabstand, der sich rechnerisch aus der 24stelligen Mantisse ergibt.
M.: Korrekt!
H.: Dann ist die Angabe von 1500 dB ja total irreführend!
M.: Zumindest mehr als verwirrend, schließlich ist dieser Wert ja nicht gleichbedeutend mit der Signal-Dynamik wie z. B. im analogen Bereich. Schau dir dazu mal diese Grafik an (M. holt aus einer Schublade das „Studio Magazin Special Rundfunktechnik“ mit dem Artikel von Dr. Ing. Udo Zölzer heraus und schlägt die Seite 35 auf).
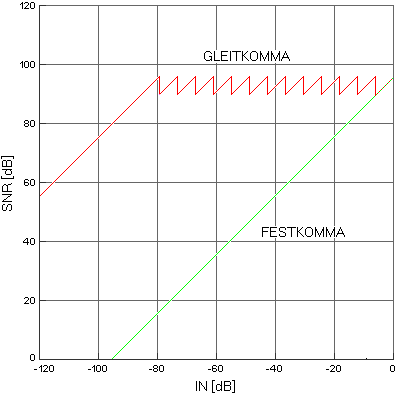
Das Diagramm zeigt den Signal-Rauschabstand über dem Eingangspegel bei einer Wortbreite von 16 Bit, einmal mit einem vierstelligen Exponenten und einmal ohne. Man sieht deutlich, daß bei beiden Darstellungen der maximal erreichbare Wert für den Signal-Rauschabstand bei ca. 96 dB liegt, folglich also nur von der Mantisse abhängt. Diese bildet also den einzigen Bezug zur analogen Signal-Dynamik, die Bitbreite des Exponenten ist dabei völlig egal.
H.: Aber wieso konstruiert man dann keinen DSP mit größerer Bitbreite in der Mantisse, indem man z. B. den Exponenten kleiner macht?
M.: Leider muß man hier einen Kompromiß schließen. Die Berechnung eines Filter-Algorithmus erfordert die Multiplikation von Zahlen und die können dann ziemlich groß werden. Außerdem möchtest du ja genügend Übersteuerungsreserve haben, um mehrere Eingangskanäle zusammenmischen zu können. Deswegen kann auf den Exponenten nicht verzichtet werden. Aber du hast vollkommen recht, manche Hersteller verwenden DSPs, die mehr als 24 Bit in der Mantisse haben und dafür weniger im Exponenten. Außerdem ist die Gesamtanzahl auch nicht auf 32 Bit festgelegt, neuere Chips verarbeiten z. B. 32 + 8, allerdings muß dann auch das gesamte Hardware-Umfeld daran angepaßt werden. Außerdem bedenke: AES/EBU arbeitet nur mit 24 Bit ohne Exponent.
H.: Wahnsinnig interessant! Rechendynamik ist also ein sehr schwammiger Begriff. Man sollte echt nicht alles glauben, was man in der Werbung liest.
M.: Das sowieso nicht, aber es genügt schon, wenn man die genauen Hintergründe kennt. Dann interpretiert man die zweifelhaften Angaben mancher Hersteller richtig.
H.: Ich werde dich jetzt bestimmt öfters konsultieren.
M.: Mach das.